Cropfaktor: Unterschied zwischen den Versionen
(Externer Link hinzu gefügt) |
K (Links aktualisiert) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 58: | Zeile 58: | ||
|} | |} | ||
<br> | <br> | ||
| − | (1) Der | + | (1) Der Cropfaktor entspricht hier dem Verhältnis der [http://de.wikipedia.org/wiki/Diagonale_%28Geometrie%29 Diagonalen] des [[Kleinbild]]formates zur [http://de.wikipedia.org/wiki/Diagonale_%28Geometrie%29 Diagonalen] der lichtempfindlichen Fläche des [[Sensor]]s. Manche Autoren beziehen diesen stattdessen auf die größere Seite des Aufnahmeformats, um den unterschiedlichen Seitenverhältnissen (2:3 bei [[Kleinbild]] und [[DSLR]], 3:4 bei den meisten Sensoren für kompakte Digitalkameras, 16:9 bei einigen neueren Modellen) gerechter zu werden. |
<br> | <br> | ||
(2) Die Größenangaben in Zoll-Bruchteilen beziehen sich traditionell auf die nutzbare Fläche von Video-Aufnahmeröhren. Eine Ein-Zoll-Vidicon-Bildröhre hat zwar 25,4 mm Außendurchmesser, jedoch nur eine nutzbare [http://de.wikipedia.org/wiki/Diagonale_%28Geometrie%29 Bilddiagonale] von etwa 16 mm. | (2) Die Größenangaben in Zoll-Bruchteilen beziehen sich traditionell auf die nutzbare Fläche von Video-Aufnahmeröhren. Eine Ein-Zoll-Vidicon-Bildröhre hat zwar 25,4 mm Außendurchmesser, jedoch nur eine nutzbare [http://de.wikipedia.org/wiki/Diagonale_%28Geometrie%29 Bilddiagonale] von etwa 16 mm. | ||
| Zeile 118: | Zeile 118: | ||
Hierzu einige Zitate aus dem [https://oly-e.fotografierer.com/?q=node/2137 hervorragenden Artikel von Reinhard Wagner in oly-e.de]: | Hierzu einige Zitate aus dem [https://oly-e.fotografierer.com/?q=node/2137 hervorragenden Artikel von Reinhard Wagner in oly-e.de]: | ||
:''"Die Brennweite eines Objektivs ist bei seiner Konstruktion festgelegt. Sie ändert sich nicht dadurch, dass man es an eine Kamera mit beliebig großem Sensor schraubt. Auch ohne Kamera hintendran hat das Objektiv genau diese Brennweite.<br><br>Die Blendenzahl eines Objektivs berechnet sich durch das Verhältnis von Brennweite zu Öffnung. Die Öffnung des Objektivs ändert sich nicht, egal, ob man das Objektiv nicht anschließt, oder an einen großen Sensor oder an einen kleinen Sensor anschließt. Sie ist eine Konstante des Objektivs, genauso wie die Brennweite.<br><br>Die Lichtstärke eines Objektivs wird durch die Blendenzahl angegeben. Sie ändert sich nicht dadurch, dass man ein anderes Aufnahmemedium dahintersetzt.<br><br>Was ändert sich durch die Änderung der Größe eines Aufnahmemediums?<br>Am Objektiv: gar nichts.<br>Am Bild in der Bildebene: gar nichts.<br><br>Der einzige Unterschied besteht darin, dass unterschiedliche Sensoren unterschiedliche Ausschnitte des Bildes wiedergeben. Ein 50mm f/1,4 hat an allen Sensoren die identische Abbildung. Es liefert nicht auf einmal eine größere Freistellung, nur weil es an einen Kleinbildsensor angeschraubt wird.<br><br>Um nun zu betrachten, welche Auswirkungen die Sensorgröße auf das Bild hat, das auf der Speicherkarte landet, nehmen wir Sensoren mit gleicher Gesamtauflösung an und gleicher Sensortechnologie.<sup>*)</sup><br>Wir nehmen des weiteren an, dass es sich beim betrachteten Objektiv um ein Objektiv handelt, dessen Bildkreis groß genug ist, um alle in Frage kommenden Sensoren auszuleuchten.<br><br>Wir betrachten als erstes die jeweiligen Schärfentiefen bei 2m Motiventfernung und 50mm f/1,4:<br>FT-Sensor: 0,031m<br>KB-Sensor: 0,062m<br>Der Kleinbildsensor liefert also eine doppelt so große (!) Schärfentiefe bei identischem Objektiv. Das hat den Grund darin, dass der zulässige Zerstreuungskreis bei einem deutlich größeren Sensor natürlich auch entsprechend größer ist.<br><br>Wir betrachten den Bildwinkel: da der FT-Sensor nur die Mitte des Bildkreises abbildet und der KB-Sensor die vierfache Fläche hat, ändert sich scheinbar (!) der Bildwinkel. In Wirklichkeit ist der Bildwinkel des Objektivs natürlich konstant. Diese scheinbare Änderung durch den Ausschnitt sieht wie folgt aus:<br>FT-Sensor: 24°<br>KB-Sensor: 48°<br><br>Damit nun eine Vergleichbarkeit gegeben ist, werden nun jeweils Objektive mit anderem Bildwinkel verwendet.<br>FT-Sensor: 25mm<br>KB-Sensor: 50mm, jeweils f/1,4<br><br>Die Schärfentiefen sehen nun folgendermaßen aus:<br>FT-Sensor: 0,126m<br>KB-Sensor: 0,062m<br><br>Um mit dem KB-Sensor die Schärfentiefe von FT zu erreichen, muss man nun auf f/2,8 abblenden. Damit wird das Bild aber nicht nur schärfer, sondern auch dunkler - und zwar genau zwei Blendenstufen. Es erreicht nur noch ein Viertel des Lichtes die einzelne Photodiode. Um diesen Lichtverlust auszugleichen, muss die Kamera die Signalverstärkung am Sensor erhöhen - also von ISO 200 auf ISO 800. Das sorgt für mehr Rauschen.<br>Prinzipbedingt hat der Kleinbildsensor aber größere Photodioden, er kann also rauschärmer gebaut werden - und zwar genau um zwei Blendenstufen. Durch das notwendige Abblenden zur Erlangung der gleichen Schärfentiefe ist aber dieser Rauschvorteil egalisiert. Ein sogenanntes Nullsummenspiel.<br><br>Fazit: Bei gleichem Bildwinkel und gleicher Blende ist die Schärfentiefe bei Kleinbild geringer. Bei gleicher Brennweite und gleicher Blende ist die Schärfentiefe bei FT geringer. Um eine identische Freistellung bei gleichem Motiv und gleicher Blende wie bei einem Kleinbildsensor zu erreichen, benötigt man bei FT eine um den Faktor ca 1,4 kleinere Brennweite. Beispiel:<br>FT: 36mm, f/2, Schärfentiefe 0,086m<br>KB: 50mm, f/2, Schärfentiefe 0,088m<br><br>Dies ist zwar eine identische Schärfentiefe, nicht jedoch ein identisches Bild, weil der Bildwinkel unterschiedlich ist. Identische Bilder wurden aber bereits einen Absatz höher behandelt. Es wird jedoch deutlich, warum es mit FT durchaus problemlos möglich ist, freizustellen.<br><br>Zur Berechnung der Schärfentiefen wurden übrigens für den FT-Sensor ein Zerstreuungskreis von 0,0071mm und für den KB-Sensor von 0,014 verwendet. Dies entspricht einer Sensorauflösung von 16MP.<br><br>Steigt nun die Sensorauflösung an, sinkt die Schärfentiefe, weil der zulässige Zerstreuungskreis sinkt.<br><br>*) Unterschiedlich große Sensoren mit gleicher Auflösung und gleicher Sensortechnologie gibt es nicht. Sie sind eine physikalische Unmöglichkeit."'' | :''"Die Brennweite eines Objektivs ist bei seiner Konstruktion festgelegt. Sie ändert sich nicht dadurch, dass man es an eine Kamera mit beliebig großem Sensor schraubt. Auch ohne Kamera hintendran hat das Objektiv genau diese Brennweite.<br><br>Die Blendenzahl eines Objektivs berechnet sich durch das Verhältnis von Brennweite zu Öffnung. Die Öffnung des Objektivs ändert sich nicht, egal, ob man das Objektiv nicht anschließt, oder an einen großen Sensor oder an einen kleinen Sensor anschließt. Sie ist eine Konstante des Objektivs, genauso wie die Brennweite.<br><br>Die Lichtstärke eines Objektivs wird durch die Blendenzahl angegeben. Sie ändert sich nicht dadurch, dass man ein anderes Aufnahmemedium dahintersetzt.<br><br>Was ändert sich durch die Änderung der Größe eines Aufnahmemediums?<br>Am Objektiv: gar nichts.<br>Am Bild in der Bildebene: gar nichts.<br><br>Der einzige Unterschied besteht darin, dass unterschiedliche Sensoren unterschiedliche Ausschnitte des Bildes wiedergeben. Ein 50mm f/1,4 hat an allen Sensoren die identische Abbildung. Es liefert nicht auf einmal eine größere Freistellung, nur weil es an einen Kleinbildsensor angeschraubt wird.<br><br>Um nun zu betrachten, welche Auswirkungen die Sensorgröße auf das Bild hat, das auf der Speicherkarte landet, nehmen wir Sensoren mit gleicher Gesamtauflösung an und gleicher Sensortechnologie.<sup>*)</sup><br>Wir nehmen des weiteren an, dass es sich beim betrachteten Objektiv um ein Objektiv handelt, dessen Bildkreis groß genug ist, um alle in Frage kommenden Sensoren auszuleuchten.<br><br>Wir betrachten als erstes die jeweiligen Schärfentiefen bei 2m Motiventfernung und 50mm f/1,4:<br>FT-Sensor: 0,031m<br>KB-Sensor: 0,062m<br>Der Kleinbildsensor liefert also eine doppelt so große (!) Schärfentiefe bei identischem Objektiv. Das hat den Grund darin, dass der zulässige Zerstreuungskreis bei einem deutlich größeren Sensor natürlich auch entsprechend größer ist.<br><br>Wir betrachten den Bildwinkel: da der FT-Sensor nur die Mitte des Bildkreises abbildet und der KB-Sensor die vierfache Fläche hat, ändert sich scheinbar (!) der Bildwinkel. In Wirklichkeit ist der Bildwinkel des Objektivs natürlich konstant. Diese scheinbare Änderung durch den Ausschnitt sieht wie folgt aus:<br>FT-Sensor: 24°<br>KB-Sensor: 48°<br><br>Damit nun eine Vergleichbarkeit gegeben ist, werden nun jeweils Objektive mit anderem Bildwinkel verwendet.<br>FT-Sensor: 25mm<br>KB-Sensor: 50mm, jeweils f/1,4<br><br>Die Schärfentiefen sehen nun folgendermaßen aus:<br>FT-Sensor: 0,126m<br>KB-Sensor: 0,062m<br><br>Um mit dem KB-Sensor die Schärfentiefe von FT zu erreichen, muss man nun auf f/2,8 abblenden. Damit wird das Bild aber nicht nur schärfer, sondern auch dunkler - und zwar genau zwei Blendenstufen. Es erreicht nur noch ein Viertel des Lichtes die einzelne Photodiode. Um diesen Lichtverlust auszugleichen, muss die Kamera die Signalverstärkung am Sensor erhöhen - also von ISO 200 auf ISO 800. Das sorgt für mehr Rauschen.<br>Prinzipbedingt hat der Kleinbildsensor aber größere Photodioden, er kann also rauschärmer gebaut werden - und zwar genau um zwei Blendenstufen. Durch das notwendige Abblenden zur Erlangung der gleichen Schärfentiefe ist aber dieser Rauschvorteil egalisiert. Ein sogenanntes Nullsummenspiel.<br><br>Fazit: Bei gleichem Bildwinkel und gleicher Blende ist die Schärfentiefe bei Kleinbild geringer. Bei gleicher Brennweite und gleicher Blende ist die Schärfentiefe bei FT geringer. Um eine identische Freistellung bei gleichem Motiv und gleicher Blende wie bei einem Kleinbildsensor zu erreichen, benötigt man bei FT eine um den Faktor ca 1,4 kleinere Brennweite. Beispiel:<br>FT: 36mm, f/2, Schärfentiefe 0,086m<br>KB: 50mm, f/2, Schärfentiefe 0,088m<br><br>Dies ist zwar eine identische Schärfentiefe, nicht jedoch ein identisches Bild, weil der Bildwinkel unterschiedlich ist. Identische Bilder wurden aber bereits einen Absatz höher behandelt. Es wird jedoch deutlich, warum es mit FT durchaus problemlos möglich ist, freizustellen.<br><br>Zur Berechnung der Schärfentiefen wurden übrigens für den FT-Sensor ein Zerstreuungskreis von 0,0071mm und für den KB-Sensor von 0,014 verwendet. Dies entspricht einer Sensorauflösung von 16MP.<br><br>Steigt nun die Sensorauflösung an, sinkt die Schärfentiefe, weil der zulässige Zerstreuungskreis sinkt.<br><br>*) Unterschiedlich große Sensoren mit gleicher Auflösung und gleicher Sensortechnologie gibt es nicht. Sie sind eine physikalische Unmöglichkeit."'' | ||
| + | |||
| + | == Interne Verweise == | ||
| + | * [[Bildwinkel]] | ||
== Weblinks == | == Weblinks == | ||
| − | *[ | + | * [https://de.wikipedia.org/wiki/Formatfaktor "Formatfaktor" in wikipedia.de] |
| − | *[ | + | * [https://pen-and-tell.de/2024/04/aequivalenz-diskussion/ "Äquivalenz-Diskussion" in pen-and-tell.de] (lesenswert) |
| − | + | * [https://lenspire.zeiss.com/photo/app/uploads/2018/04/Article-Bokeh-2010-DE.pdf "Schärfentiefe und Bokeh" von Dr. Hubert Nasse (Carl Zeiss - Geschäftsbereich Photo-Objektive), März 2010] (PDF - lesenswert) | |
| − | + | * [https://www.dslr-forum.de/threads/zur-brennweite-und-zum-crop.21047/#post-196926 Ausführliche Erklärung im dslr-Forum] (lesenswert) | |
| − | + | * [https://www.youtube.com/watch?v=om5iffxLYPM "Brennweite bei MFT, APS-C und VF - Der Cropfaktor" bei Krolop & Gerst] (Video - sehenswert) | |
| − | + | * [https://www.dpreview.com/articles/2666934640/what-is-equivalence-and-why-should-i-care "What is equivalence and why should I care?" bei dpreview.com] (englisch) | |
| − | *[https://lenspire.zeiss.com/photo/app/uploads/2018/04/Article-Bokeh-2010-DE.pdf "Schärfentiefe und Bokeh" von Dr. Hubert Nasse (Carl Zeiss - Geschäftsbereich Photo-Objektive), März 2010] | ||
| − | *[https://www.youtube.com/watch?v=om5iffxLYPM "Brennweite bei MFT, APS-C und VF - Der Cropfaktor" bei Krolop & Gerst] (Video - sehenswert) | ||
| − | |||
| − | |||
| − | |||
[[Category:Fachbegriffe]] | [[Category:Fachbegriffe]] | ||
[[Kategorie:Altglas]] | [[Kategorie:Altglas]] | ||
Aktuelle Version vom 3. April 2024, 17:21 Uhr
Begriffserklärung
Der Cropfaktor gibt das Längenverhältnis zwischen den Diagonalen zweier Aufnahmeformate (flächenmäßige Bildgröße) an. Als Basis (also die "1") wurde von der Fachpresse das Kleinbildformat (24 x 36 mm) festgelegt.
Dies bedeutet:
- Bei einem Cropfaktor größer als "1" ist das Aufnahmeformat kleiner als das (als Basis) festgelegte Kleinbildformat.
- Bei einem Cropfaktor kleiner als "1" ist das Aufnahmeformat größer als das (als Basis) festgelegte Kleinbildformat.
Eine Aussage über die Qualität der Aufnahme (in Abhängigkeit des Aufnahmemediums (Sensor bzw. Film)) kann vom Cropfaktor nicht abgeleitet werden, da die Größe des Sensors nur einer von vielen Faktoren zur Bestimmung der Bildgüte ist. Erst im Zusammenwirken aller Einflussgrößen - wie Objektiv (hierbei ist die Korrektur der Abbildungsfehler entscheidend), Güte der Mikrolinsen, interne Bildverarbeitungsalgorithmen, entsprechende Bildbearbeitung und vieles Andere mehr - wird die gewünschte hervorragende Bildgüte erreicht.
Da Aufnahmeformat, Bildwinkel und Brennweite über den Strahlensatz zusammenhängen, kann der Cropfaktor (besser: Formatfaktor) dazu genutzt werden, zu berechnen, welche Brennweite ein Objektiv haben müsste, um auf einem anderen Aufnahmeformat den gleichen Bildwinkel, also bei gleicher Entfernung zum Motiv den gleichen Bildausschnitt zu zeigen.
Der Cropfaktor ist auch ein Brennweitenverlängerungsfaktor. Um denselben Bildwinkel und die gleiche Perspektivische Tiefe zu erhalten benötigt man bei Kleinbild bezogen auf FourThirds die doppelte Brennweite. Ein 400 mm Teleobjektiv bei Kleinbild entspricht im Bildwinkel einem 200 mm bei FourThirds.
Der Cropfaktor hat über die Brennweite auch einen Einfluss auch die Schärfentiefe, die beim Four Thirds System größer ist, als bei Kleinbild.
Zitate
Ein Zitat von Dr. Hubert Nasse (Carl Zeiss - Geschäftsbereich Photo-Objektive) aus seiner Veröffentlichung "Schärfentiefe und Bokeh", Camera Lens News 35 (März 2010):
- "Wenn wir ein Objektiv von einer alten analogen Kamera abnehmen und stattdessen an eine Digitalkamera des gleichen Systems ansetzen, die aber den etwas kleineren APS-C-Sensor enthält, dann sprechen wir ja von einem "Crop-Faktor", wir hätten auch einfach sagen können, dass der kleine Sensor automatisch eine Ausschnittsvergrößerung macht, wenn wir am gleichen Standpunkt stehen bleiben. Den Ausdruck "Brennweitenverlängerung" wollen wir lieber nicht benutzen, denn die gibt es nicht - das Objektiv weiß ja nicht, wie viel von seinem Bildkreis wir mit unserem Sensor einfangen."
Ein sehr schönes Zitat von David Thorpe über Sinn und Unsinn des Vergleichs von Objektiven mit unterschiedlichen Bildkreisen (FT, Kleinbild, Mittelformat etc.) u.a. hinsichtlich der Schärfentiefe:
- "Equivalence. It’s the bugbear of anyone who reviews Micro Four Thirds lenses. You are being conned says the incoming mail. Your f/1.4 lens is really an f/2.8. And your so called shallow depth of field is commensurate with f/2.8, too, not f/1.4. It’s an argument I’ve heard so many times and while factually true, is pointless and irrelevant. The only rational response is -so what?"
"Put simply, a native Micro Four Thirds lens is just that. A native Micro Four Thirds lens. It isn’t a Full Frame lens. It won’t fit a DSLR and if it did it wouldn’t cover the whole frame. I’ve tried more and more to describe lenses according to their angle of view since that is universal. If you know what angle of view you want, you can choose a lens to get it. Thus, I know that I like as a standard prime a lens with a moderate wide angle, around 54° horizontal. A quick calculation at Points In Focus Photography tells me that for a DSLR it would be 17mm, for FF 35mm and for Medium Format 55mm. Easy."
"Not so easy for depth of field. I hear from people who are quite obsessed with getting shallow depth of field. Medium Format is the real answer as anyone who has used Hasselblads will know. The Sonnar 150mm f/4 short tele let you photograph someone full length and splat the background totally. But for most with that obsession, Micro Four Thirds is the wrong choice of format. A more practical and adequate choice would be a DSLR with its 36x24mm sensor. But human nature doesn’t work that way. Come to think f it, nor does animal nature. I remember photographing some sheep grazing in a grassy field. I was there a couple of hours and noticed how some of the sheep would try to get under the wire fence to get to the next field. If they couldn’t, they would stretch themselves out and eat the grass the could reach under the fence."
"The point was, the field next door was exactly the same as the field they were in. It was just as grassy and it was just as green. That I reckon, is why photographers buy Micro Four Thirds and then complain about too much depth of field. What do I want? Whatever I can’t have!"
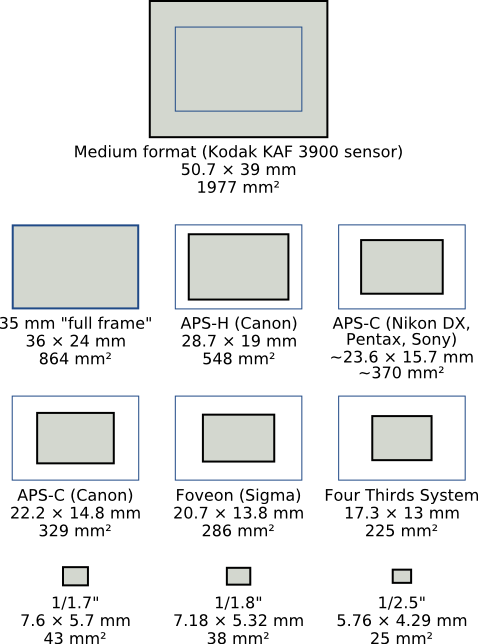
Cropfaktoren gängiger Sensorgrößen relativ zum Kleinbildformat
| Faktor (1) | Sensorgröße | Typische Auflösung | Diagonale | Fläche bezogen auf Kleinbild |
|---|---|---|---|---|
| 8,7 | 1/3,2" | ca. 2 - 3 Megapixel | 5 mm (2) | 1,3% |
| 8 | 1/3" (Manche Videokameras) | 1,5% | ||
| 7,2 | 1/2,7" | ca. 3 - 5 Megapixel | 6 mm (2) | 1,9% |
| 6,8 | 1/2,5" | ca. 3 - 12 Megapixel | 6,4 mm (2) | 2,2% |
| 4,9 | 1/1,8" | ca. 4 - 15 Megapixel | 8,9 mm (2) | 4% |
| 4 | 2/3" | ca. 8 Megapixel | 11 mm (2) | 6,5% |
| 2 | 4/3" entsp. FourThirds | ab 5 Megapixel | 21,3 mm (2) | 25% |
| 1,6 | entsprechend APS-C (Canon) | ab 6 Megapixel | 27,1 mm | 39% |
| 1,5 | entsprechend DX (Nikon etc.) | ab 6 Megapixel | 28,3 mm | 44% |
| 1,3 | entsprechend APS-H (z. B. Canon EOS 1D MKIV) | ab 8 Megapixel | 34,7 mm | 59% |
| 1 | Kleinbild-Vollformat, FX | ab 6 Megapixel | 43,3 mm | 100% |
| 0,55 | Mittelformat (56 x 56 mm) | - | 79,2 mm | 205% |
| 0,49 | Mittelformat (Pentax 6x7, 55 x 70 mm) | - | 89,0 mm | 205% |
(1) Der Cropfaktor entspricht hier dem Verhältnis der Diagonalen des Kleinbildformates zur Diagonalen der lichtempfindlichen Fläche des Sensors. Manche Autoren beziehen diesen stattdessen auf die größere Seite des Aufnahmeformats, um den unterschiedlichen Seitenverhältnissen (2:3 bei Kleinbild und DSLR, 3:4 bei den meisten Sensoren für kompakte Digitalkameras, 16:9 bei einigen neueren Modellen) gerechter zu werden.
(2) Die Größenangaben in Zoll-Bruchteilen beziehen sich traditionell auf die nutzbare Fläche von Video-Aufnahmeröhren. Eine Ein-Zoll-Vidicon-Bildröhre hat zwar 25,4 mm Außendurchmesser, jedoch nur eine nutzbare Bilddiagonale von etwa 16 mm.
Cropfaktor als "Systemstreit"
Der Cropfaktor ist ein Punkt im Disput von Anhängern unterschiedlicher Hersteller. Hier eine Sammlung von Argumenten und Scheinargumenten im Zusammenhang mit dem Cropfaktor und der Versuch, Missverständnisse und verdrehte Tatsachen klarzustellen.
Ein großer Cropfaktor bedeutet (automatisch) eine schlechtere Bildqualität
Gründe für das Argument
Auf den ersten Blick scheint das korrekt zu sein:
- kleine Fläche des Sensors (bzw. Films) - schlechte Bildqualität
- große Fläche des Sensors (bzw. Films) - gute Bildqualität
Als Indiz dafür werden sehr gerne Erfahrungen aus der "analogen Zeit" hinzugezogen - man denke an die Erfahrungen mit den ominösen "Pocket-Kameras" im Vergleich zum Kleinbildformat. Hierbei war die Bildqualität augenscheinlich viel schlechter als die des 24 x 36 mm-Formats.
Analog: Vergleich des "Pocket-" und des Kleinbild-Formats
Hierzu ist aber eine genauere Betrachtung einzelner Faktoren - die zur entsprechenden Bildqualität führen - notwendig:
- gängige "Pocket"
Alle genannten Faktoren ließen Prints bis zu einer Größe von 10 x 15cm ("Postkartenformat") zu, dies war für die damalige Käuferschicht vollkommen ausreichend.
- gängige SLR-Kamera (z. B. Olympus OM-1 mit dem Normalobjektiv (Zuiko Auto-S 1:1,8/50 mm) - eine gängige und vielfach verkaufte Kombination aus der Zeit)
- Film-Format 24 x 36 mm
- Objektiv hervorragender Qualität
- normal auflösender Film
- hervorragende Planlage des Films
Durch das Zusammenwirken dieser Faktoren konnten ohne Probleme Prints in einer Größe von 50 x 75 cm produziert werden. Hier stimmt also die obrige Aussage: Kleine Fläche - schlechte Qualität / große Fläche - gute Qualität.
Digital: Vergleich des FT- und des APS-C-Formats
Nun wenden wir diesen Vergleich auf die derzeitige digitale Technik an:
Vergleicht man - anhand von "Groß-Prints" (ab 80 x 120 cm) die resultierende Bildqualität, so wird man nur sehr kleine Unterschiede feststellen, diese resultieren eher aus den herstellerspezifischen Vorlieben bei der Gewichtung der Parameter in den internen Bildverarbeitungsalgorithmen - Geschmackssache also.
Hier stimmt also die obrige Aussage nicht: Kleine Fläche - schlechte Qualität / große Fläche - gute Qualität. Die Qualität ist - bis auf die o. g. kleinen (herstellerspezifischen) Unterschiede - vergleichbar.
Fehlerhaftes Zusammenspiel der Faktoren zur Erzielung der Bildqualität
Stimmt das Zusammenwirken aller Faktoren nicht, so resultiert eine schlechte Bildqualität - hierzu zwei Beispiele:
- Es kann noch so ein guter Sensor in der Kamera vorhanden sein, bei einer schlechten Abbildungsleistung des Objektives (d. h. fehlerhafte Korrektur der Abbildungsfehler) kann kein vernünftiges Bildergebnis entstehen - ich denke hier z. B. an die "Billig-Kompakt-Kameras", die trotz eines 12-Megapixel-Sensors nur ca. 6 Megapixel effektiv auflösen können (vergleichbare "Marken-Kameras" erreichen dagegen effektiv ca. 10 Megapixel).
- Ein nicht auf den Bildkreis abgestimmtes Objektiv - wie z. B. ein Mittelformat-Objektiv - kann bei einem ungeeigneten Sensor (z. B. ein FT-Sensor) kein "Auflösungswunder" erzielen, da es gar nicht auf die Auflösung des FT-Sensors gerechnet ist - die Auflösung ist einfach viel zu gering!
Bei sehr kleinen Sensoren (z. B. in "Handy-Kameras") resultiert die schlechte Bildqualität - trotz "sehr viel Megapixel" - meist aus ungeeigneten "Objektiven", die solch kleine Strukturen einfach nicht auflösen können.
Schlussfolgerung
Der Cropfaktor ist eigentlich nur dafür geeignet, die Bildwinkel der Objektive bei verschiedenen Sensorgrößen zu vergleichen - nicht mehr und nicht weniger. Eine Aussage über die Bildqualität ist so nicht möglich.
FT hat einen wesentlich kleineren Cropfaktor gegenüber APS-C
Der Unterschied zwischen einem FT-Sensor und einem APS-C-Sensor (Cropfaktor 1,5 bis 1,7) ist nicht so dramatisch, wie oft dargestellt, Einzelheiten s. in der o. a. Tabelle.
Äquivalenzbrennweite und -blende
Hierzu einige Zitate aus dem hervorragenden Artikel von Reinhard Wagner in oly-e.de:
- "Die Brennweite eines Objektivs ist bei seiner Konstruktion festgelegt. Sie ändert sich nicht dadurch, dass man es an eine Kamera mit beliebig großem Sensor schraubt. Auch ohne Kamera hintendran hat das Objektiv genau diese Brennweite.
Die Blendenzahl eines Objektivs berechnet sich durch das Verhältnis von Brennweite zu Öffnung. Die Öffnung des Objektivs ändert sich nicht, egal, ob man das Objektiv nicht anschließt, oder an einen großen Sensor oder an einen kleinen Sensor anschließt. Sie ist eine Konstante des Objektivs, genauso wie die Brennweite.
Die Lichtstärke eines Objektivs wird durch die Blendenzahl angegeben. Sie ändert sich nicht dadurch, dass man ein anderes Aufnahmemedium dahintersetzt.
Was ändert sich durch die Änderung der Größe eines Aufnahmemediums?
Am Objektiv: gar nichts.
Am Bild in der Bildebene: gar nichts.
Der einzige Unterschied besteht darin, dass unterschiedliche Sensoren unterschiedliche Ausschnitte des Bildes wiedergeben. Ein 50mm f/1,4 hat an allen Sensoren die identische Abbildung. Es liefert nicht auf einmal eine größere Freistellung, nur weil es an einen Kleinbildsensor angeschraubt wird.
Um nun zu betrachten, welche Auswirkungen die Sensorgröße auf das Bild hat, das auf der Speicherkarte landet, nehmen wir Sensoren mit gleicher Gesamtauflösung an und gleicher Sensortechnologie.*)
Wir nehmen des weiteren an, dass es sich beim betrachteten Objektiv um ein Objektiv handelt, dessen Bildkreis groß genug ist, um alle in Frage kommenden Sensoren auszuleuchten.
Wir betrachten als erstes die jeweiligen Schärfentiefen bei 2m Motiventfernung und 50mm f/1,4:
FT-Sensor: 0,031m
KB-Sensor: 0,062m
Der Kleinbildsensor liefert also eine doppelt so große (!) Schärfentiefe bei identischem Objektiv. Das hat den Grund darin, dass der zulässige Zerstreuungskreis bei einem deutlich größeren Sensor natürlich auch entsprechend größer ist.
Wir betrachten den Bildwinkel: da der FT-Sensor nur die Mitte des Bildkreises abbildet und der KB-Sensor die vierfache Fläche hat, ändert sich scheinbar (!) der Bildwinkel. In Wirklichkeit ist der Bildwinkel des Objektivs natürlich konstant. Diese scheinbare Änderung durch den Ausschnitt sieht wie folgt aus:
FT-Sensor: 24°
KB-Sensor: 48°
Damit nun eine Vergleichbarkeit gegeben ist, werden nun jeweils Objektive mit anderem Bildwinkel verwendet.
FT-Sensor: 25mm
KB-Sensor: 50mm, jeweils f/1,4
Die Schärfentiefen sehen nun folgendermaßen aus:
FT-Sensor: 0,126m
KB-Sensor: 0,062m
Um mit dem KB-Sensor die Schärfentiefe von FT zu erreichen, muss man nun auf f/2,8 abblenden. Damit wird das Bild aber nicht nur schärfer, sondern auch dunkler - und zwar genau zwei Blendenstufen. Es erreicht nur noch ein Viertel des Lichtes die einzelne Photodiode. Um diesen Lichtverlust auszugleichen, muss die Kamera die Signalverstärkung am Sensor erhöhen - also von ISO 200 auf ISO 800. Das sorgt für mehr Rauschen.
Prinzipbedingt hat der Kleinbildsensor aber größere Photodioden, er kann also rauschärmer gebaut werden - und zwar genau um zwei Blendenstufen. Durch das notwendige Abblenden zur Erlangung der gleichen Schärfentiefe ist aber dieser Rauschvorteil egalisiert. Ein sogenanntes Nullsummenspiel.
Fazit: Bei gleichem Bildwinkel und gleicher Blende ist die Schärfentiefe bei Kleinbild geringer. Bei gleicher Brennweite und gleicher Blende ist die Schärfentiefe bei FT geringer. Um eine identische Freistellung bei gleichem Motiv und gleicher Blende wie bei einem Kleinbildsensor zu erreichen, benötigt man bei FT eine um den Faktor ca 1,4 kleinere Brennweite. Beispiel:
FT: 36mm, f/2, Schärfentiefe 0,086m
KB: 50mm, f/2, Schärfentiefe 0,088m
Dies ist zwar eine identische Schärfentiefe, nicht jedoch ein identisches Bild, weil der Bildwinkel unterschiedlich ist. Identische Bilder wurden aber bereits einen Absatz höher behandelt. Es wird jedoch deutlich, warum es mit FT durchaus problemlos möglich ist, freizustellen.
Zur Berechnung der Schärfentiefen wurden übrigens für den FT-Sensor ein Zerstreuungskreis von 0,0071mm und für den KB-Sensor von 0,014 verwendet. Dies entspricht einer Sensorauflösung von 16MP.
Steigt nun die Sensorauflösung an, sinkt die Schärfentiefe, weil der zulässige Zerstreuungskreis sinkt.
*) Unterschiedlich große Sensoren mit gleicher Auflösung und gleicher Sensortechnologie gibt es nicht. Sie sind eine physikalische Unmöglichkeit."
Interne Verweise
Weblinks
- "Formatfaktor" in wikipedia.de
- "Äquivalenz-Diskussion" in pen-and-tell.de (lesenswert)
- "Schärfentiefe und Bokeh" von Dr. Hubert Nasse (Carl Zeiss - Geschäftsbereich Photo-Objektive), März 2010 (PDF - lesenswert)
- Ausführliche Erklärung im dslr-Forum (lesenswert)
- "Brennweite bei MFT, APS-C und VF - Der Cropfaktor" bei Krolop & Gerst (Video - sehenswert)
- "What is equivalence and why should I care?" bei dpreview.com (englisch)